Skip to contents

Aquifer steps

aquifer.Rmd

Generalized radial flow model (Barker, 1988) 

time <- as.numeric(1:2000)
flow_rate <- c(rep(0.001, 500),
                rep(0.002, 500),
                rep(0.0, 1000))

# radial (flow_dimension = 2 Theis)
dat <- data.frame(time = time,
                  flow_rate = flow_rate)
formula <- as.formula(flow_rate~time)
grf = recipe(formula = formula, data = dat) |>
  step_aquifer_grf(time = time,
                   flow_rate = flow_rate,
                   thickness = 1.0,
                   radius = 20.0,
                   specific_storage = 1e-5,
                   hydraulic_conductivity = 1e-3,
                   flow_dimension = 2) |>
  plate()


plot(aquifer_grf~time, grf,
     type = "l", 
     ylab = "drawdown", 
     xlab = "")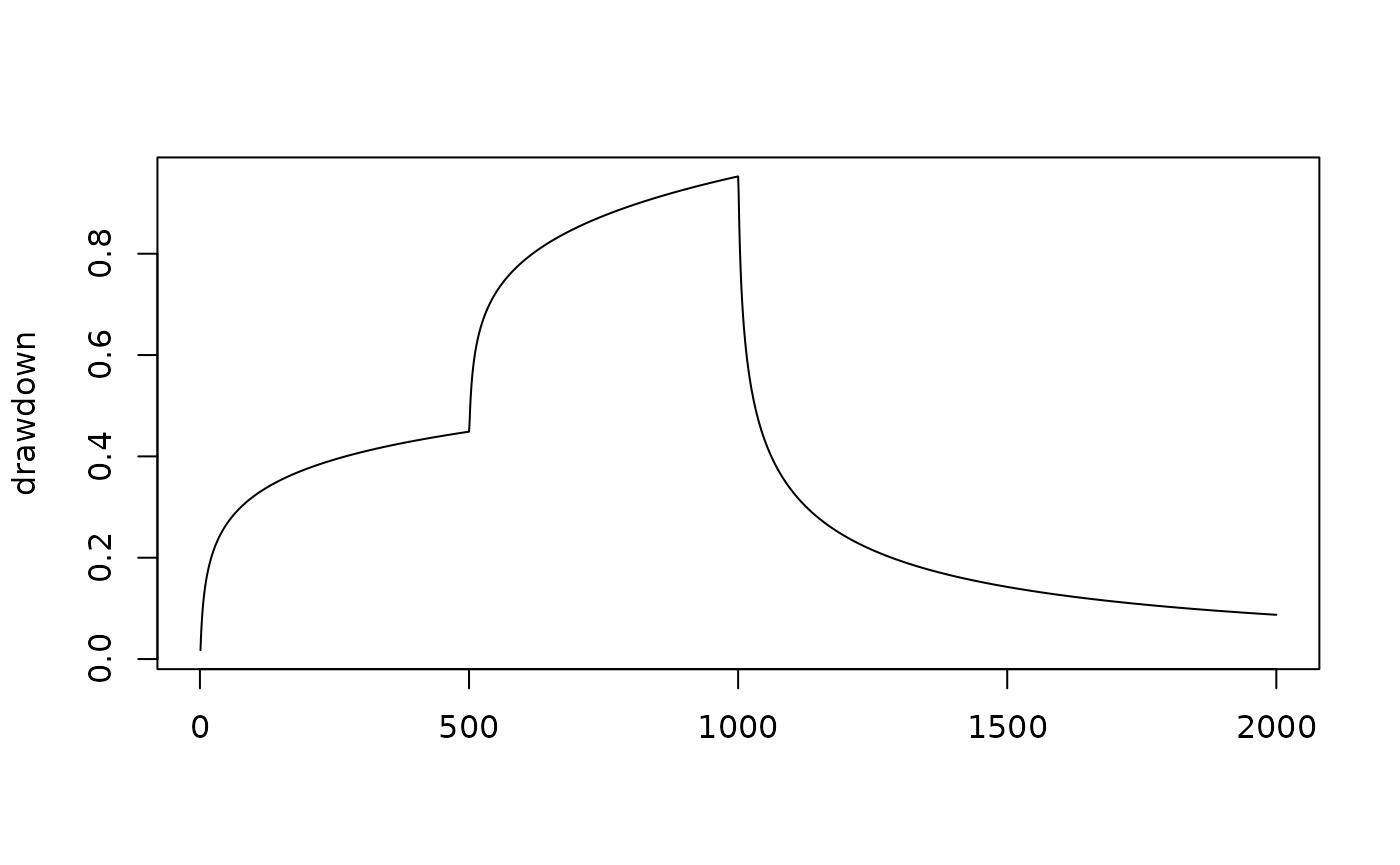

Drawdown curves determined using two pumping rates and radial flow. A recovery period is following the pumping is included.

Anisotropic Theis flow model (Papadopulos, 1965) 


# along major direction
theis_aniso_x <- recipe(formula = formula, data = dat) |>
  step_aquifer_theis_aniso(time = time,
                   flow_rate = flow_rate,
                   thickness = 1.0,
                   distance_x = 20,
                   distance_y = 0,
                   specific_storage = 1e-5,
                   hydraulic_conductivity_major = 1.0e-3,
                   hydraulic_conductivity_minor = 1.0e-4,
                   major_axis_angle = 0.0) |>
  plate()

# along minor direction
theis_aniso_y <- recipe(formula = formula, data = dat) |>
  step_aquifer_theis_aniso(time = time,
                   flow_rate = flow_rate,
                   thickness = 1.0,
                   distance_x = 0,
                   distance_y = 20,
                   specific_storage = 1e-5,
                   hydraulic_conductivity_major = 1.0e-3,
                   hydraulic_conductivity_minor = 1.0e-4,
                   major_axis_angle = 0.0) |>
  plate()

# midway between minor and major
theis_aniso_xy <- recipe(formula = formula, data = dat) |>
  step_aquifer_theis_aniso(time = time,
                   flow_rate = flow_rate,
                   thickness = 1.0,
                   distance_x = 20 / (sqrt(2)),
                   distance_y = 20 / (sqrt(2)),
                   specific_storage = 1e-5,
                   hydraulic_conductivity_major = 1.0e-3,
                   hydraulic_conductivity_minor = 1.0e-4,
                   major_axis_angle = 0.0) |>
  plate()

# isotropic higher K
theis_aniso_iso_high <- recipe(formula = formula, data = dat) |>
  step_aquifer_theis_aniso(time = time,
                   flow_rate = flow_rate,
                   thickness = 1.0,
                   distance_x = 20,
                   distance_y = 0,
                   specific_storage = 1e-5,
                   hydraulic_conductivity_major = 1.0e-3,
                   hydraulic_conductivity_minor = 1.0e-3,
                   major_axis_angle = 0.0) |>
  plate()
# isotropic lower K
theis_aniso_iso_low <- recipe(formula = formula, data = dat) |>
  step_aquifer_theis_aniso(time = time,
                   flow_rate = flow_rate,
                   thickness = 1.0,
                   distance_x = 20,
                   distance_y = 0,
                   specific_storage = 1e-5,
                   hydraulic_conductivity_major = 1.0e-4,
                   hydraulic_conductivity_minor = 1.0e-4,
                   major_axis_angle = 0.0) |>
  plate()


plot(aquifer_theis_aniso~time, theis_aniso_iso_low,
     type = "l", 
     ylab = "drawdown", 
     xlab = "",
     lty = 2,
     col = "red")
points(aquifer_theis_aniso~time, theis_aniso_iso_high,
     type = "l", 
     ylab = "drawdown", 
     xlab = "",
     lty = 2)

points(aquifer_theis_aniso~time, theis_aniso_x,
     type = "l", 
     ylab = "drawdown", 
     xlab = "")
points(aquifer_theis_aniso~time, theis_aniso_y,
     type = "l", 
     ylab = "drawdown", 
     xlab = "", 
     col = "red")
points(aquifer_theis_aniso~time, theis_aniso_xy,
     type = "l", 
     ylab = "drawdown", 
     xlab = "", 
     col = "blue")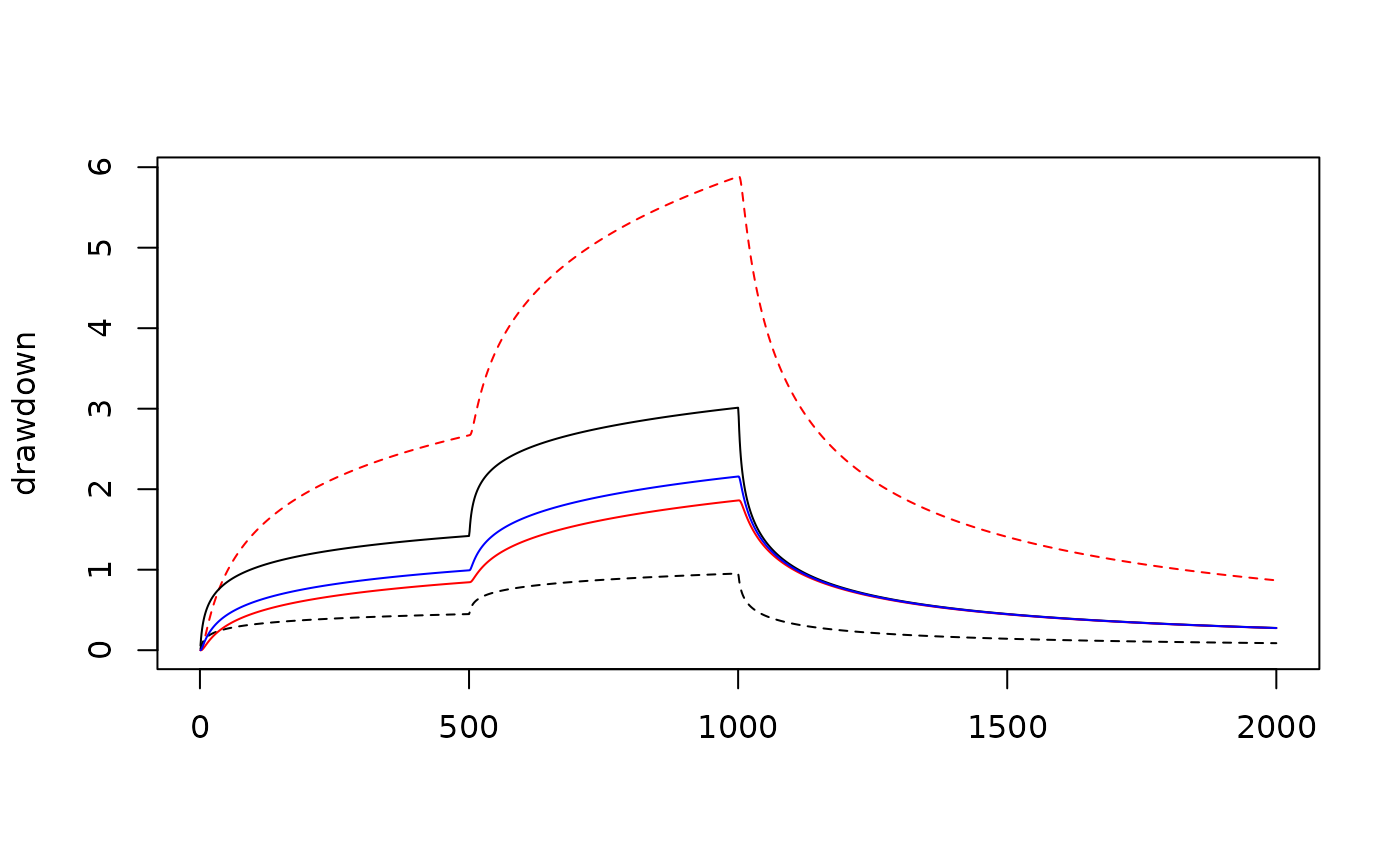

A series of anisotropic Theis drawdown and recovery curves for monitoring wells with different orientations to the major and minor axes.



# Early time
plot(aquifer_theis_aniso~time, theis_aniso_iso_low,
     type = "l", 
     ylab = "drawdown", 
     xlab = "",
     lty = 2, 
     xlim = c(0, 50),
     ylim = c(0, 1),
     col = "red")
points(aquifer_theis_aniso~time, theis_aniso_iso_high,
     type = "l", 
     ylab = "drawdown", 
     xlab = "",
     lty = 2)

points(aquifer_theis_aniso~time, theis_aniso_x,
     type = "l", 
     ylab = "drawdown", 
     xlab = "")
points(aquifer_theis_aniso~time, theis_aniso_y,
     type = "l", 
     ylab = "drawdown", 
     xlab = "", 
     col = "red")
points(aquifer_theis_aniso~time, theis_aniso_xy,
     type = "l", 
     ylab = "drawdown", 
     xlab = "", 
     col = "blue")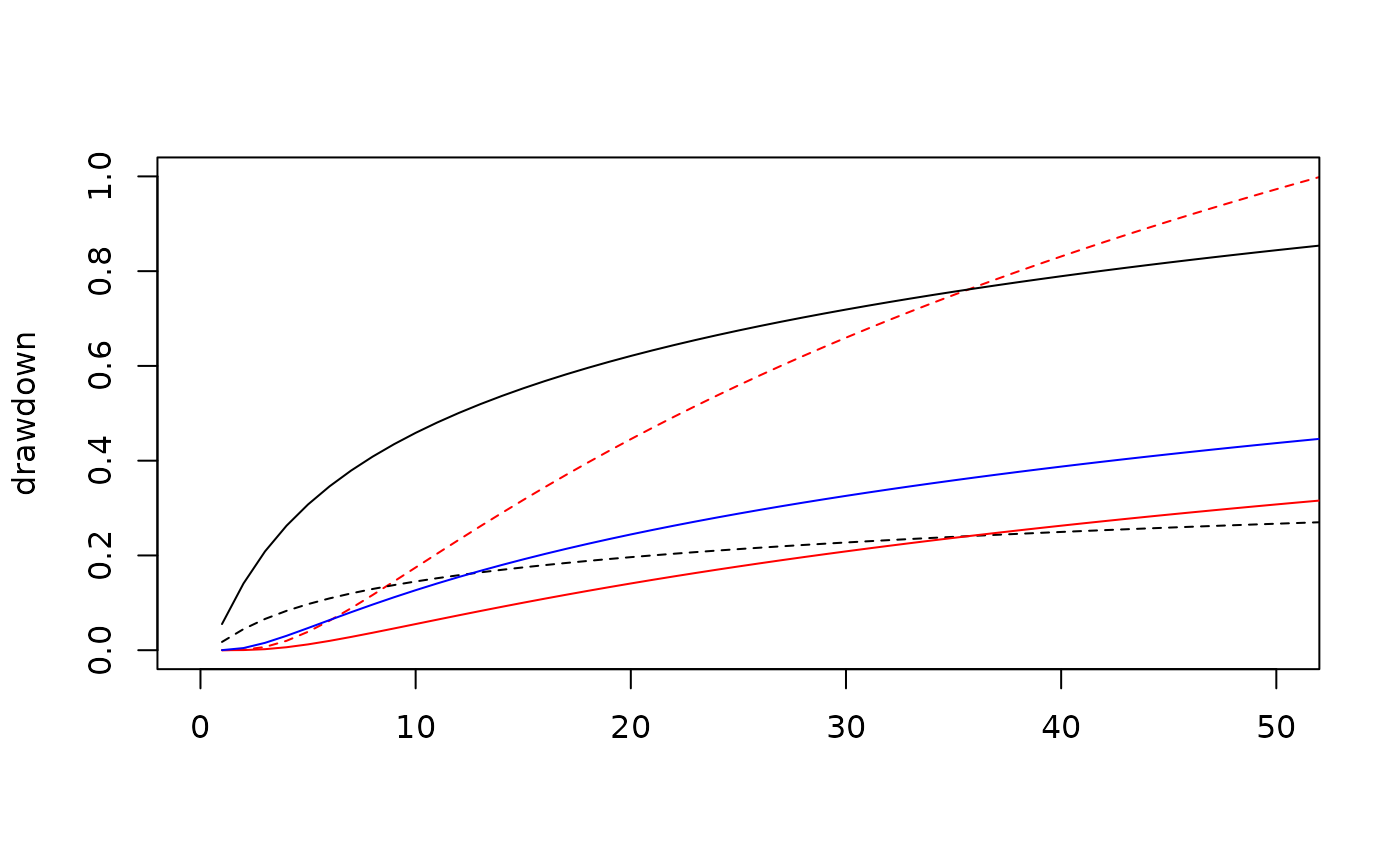

A series of anisotropic Theis drawdown and recovery curves for monitoring wells with different orientations to the major and minor axes.

Hantush-Jacob leaky aquifer (Hantush-Jacob, 1955) 



# high
hj <- recipe(formula = formula, data = dat) |>
  step_aquifer_leaky(time, 
                     flow_rate, 
                     leakage = 100, 
                     radius = 100, 
                     storativity = 1e-6,
                     transmissivity = 1e-4) |> 
  plate()

plot(aquifer_leaky~time, hj, type = "l", 
     ylab = "drawdown", 
     xlab = "")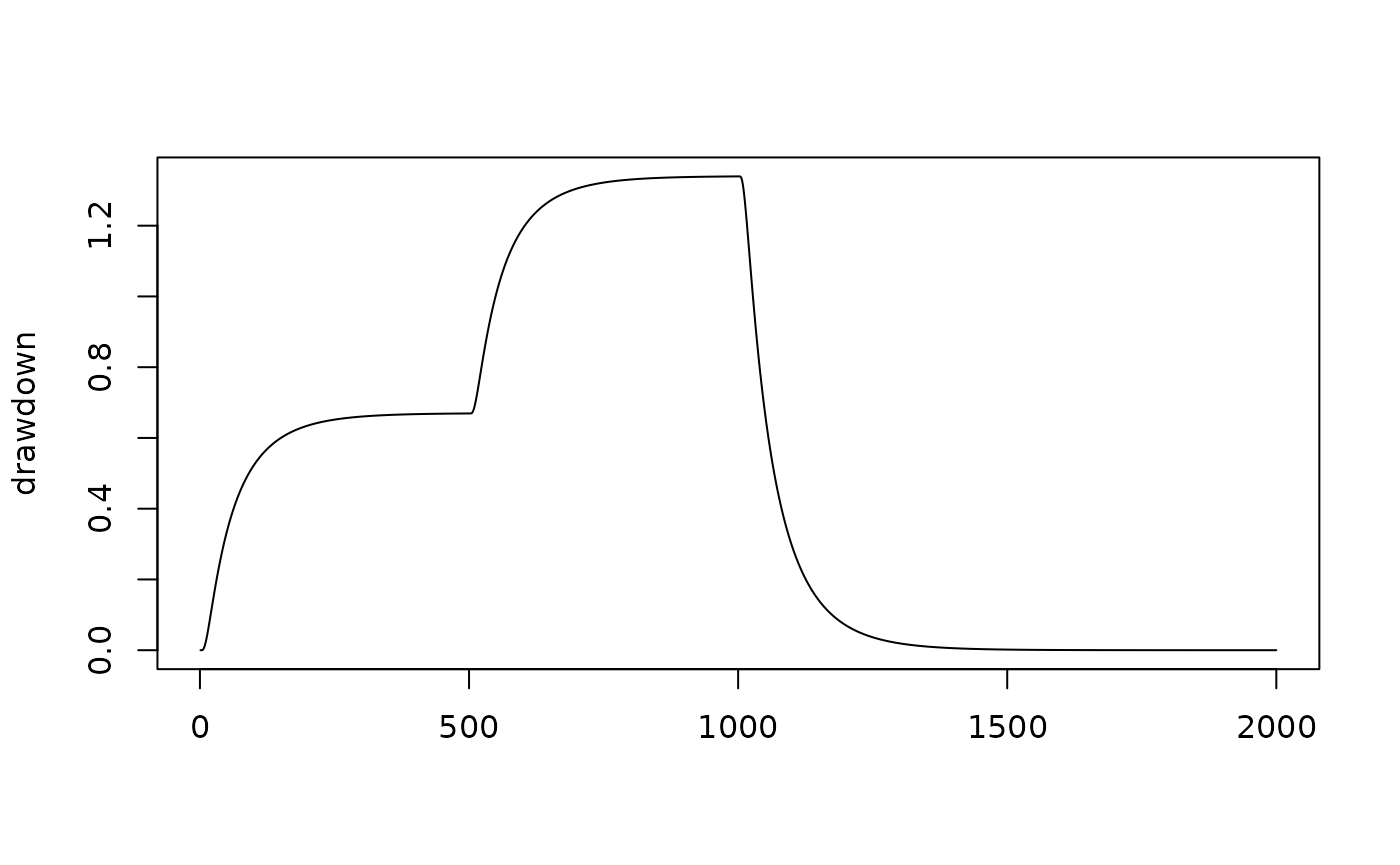

Drawdown curves determined using two pumping rates and the Hantush-Jacob solution.

Barker-Herbert radially symmetric patch (Barker-Herbert, 1982)

Figure 2 


formula <- as.formula(flow_rate~time)
q <- 0.05
t_1 <- 1.0
t_2 <- 1.0
s_1 <- 1e-5
s_2 <- 1e-7
r <- 10
R <- 100
time <- 10^seq(-4, 4, 0.01)
dat <- data.frame(time = time)

bh = recipe(formula = formula, data = dat) |>
  step_aquifer_patch(time = time, 
                     flow_rate = q,
                     thickness = 1.0,
                     radius = r,
                     radius_patch = R,
                     specific_storage_inner = s_1,
                     specific_storage_outer = s_2,
                     hydraulic_conductivity_inner = t_1,
                     hydraulic_conductivity_outer = t_2,
                     n_stehfest = 12L) |>
  plate()

dim_time_scale = (4.0 * t_1) / (s_1 * r^2)
dim_s_scale = 4.0 * pi * t_1 / q
bh$dim_time <- bh$time * dim_time_scale
bh$dim_s <- bh$aquifer_patch * dim_s_scale

plot(dim_s~dim_time, bh, type = "l", 
     ylab = "drawdown (dimensionless)", 
     xlab = "time (dimensionless)",
     log = "x",
     ylim = c(0, 50))

bh = recipe(formula = formula, data = dat) |>
  step_aquifer_patch(time = time, 
                     flow_rate = q,
                     thickness = 1.0,
                     radius = r,
                     radius_patch = R,
                     specific_storage_inner = s_1,
                     specific_storage_outer = s_2,
                     hydraulic_conductivity_inner = t_1,
                     hydraulic_conductivity_outer = t_2 * 10,
                     n_stehfest = 12L) |>
  plate()

dim_time_scale = (4.0 * t_1) / (s_1 * r^2)
dim_s_scale = 4.0 * pi * t_1 / q
bh$dim_time <- bh$time * dim_time_scale
bh$dim_s <- bh$aquifer_patch * dim_s_scale


points(dim_s~dim_time, bh, type = "l")

t_1 <- t_1 * 10.0
bh = recipe(formula = formula, data = dat) |>
  step_aquifer_patch(time = time, 
                     flow_rate = q,
                     thickness = 1.0,
                     radius = r,
                     radius_patch = R,
                     specific_storage_inner = s_1,
                     specific_storage_outer = s_2,
                     hydraulic_conductivity_inner = t_1,
                     hydraulic_conductivity_outer = t_2,
                     n_stehfest = 12L) |>
  plate()

dim_time_scale = (4.0 * t_1) / (s_1 * r^2)
dim_s_scale = (4.0 * pi * t_1) / q
bh$dim_time <- bh$time * dim_time_scale
bh$dim_s <- bh$aquifer_patch * dim_s_scale


points(dim_s~dim_time, bh, type = "l")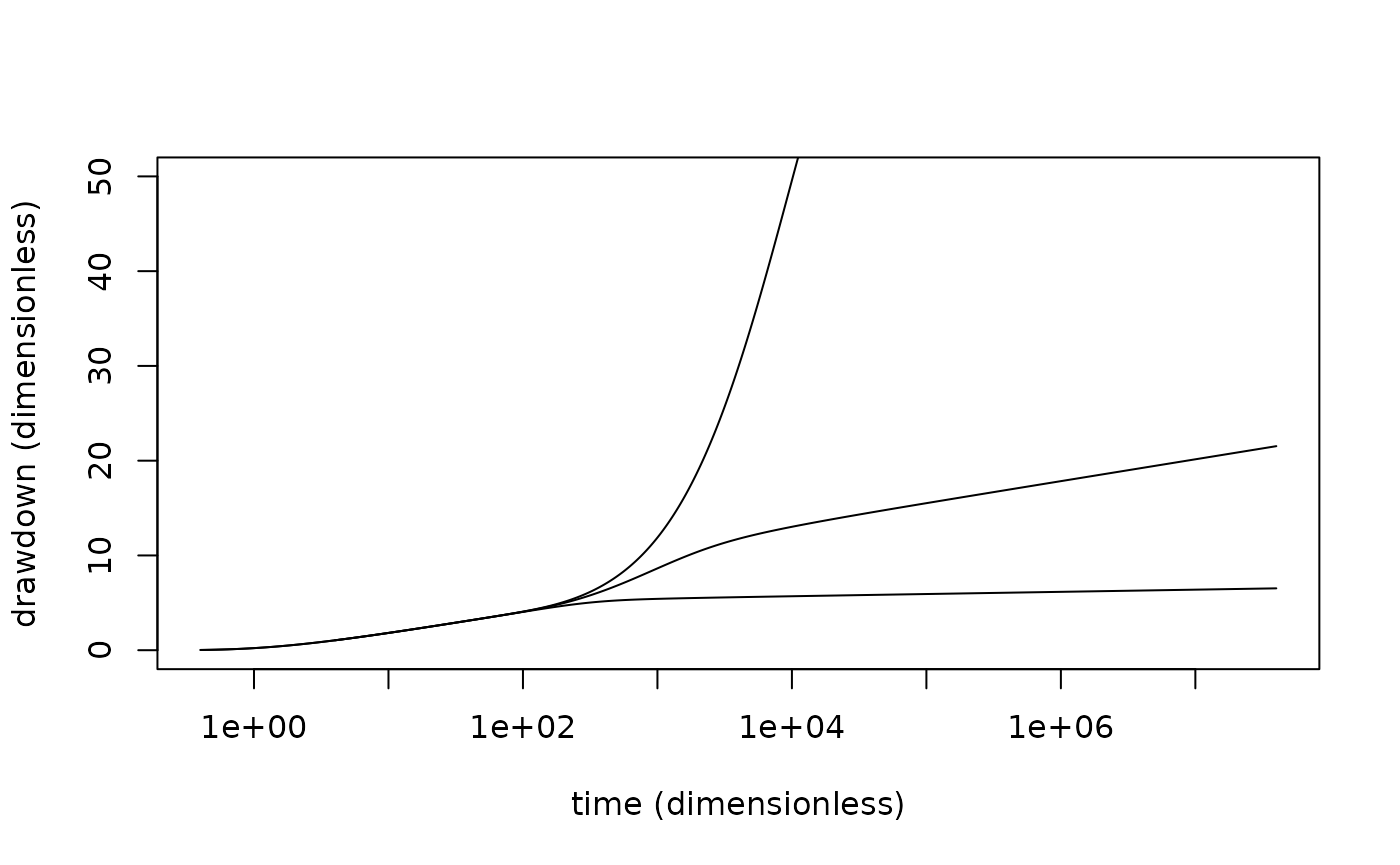

Dimensionless drawdown curves to match the Barker-Herbert, 1982 figure 2.

Figure 3 


formula <- as.formula(flow_rate~time)
t_1 <- 1.0
t_2 <- 1.0
s_1 <- 1e-5
s_2 <- 1e-5

bh = recipe(formula = formula, data = dat) |>
  step_aquifer_patch(time = time, 
                     flow_rate = q,
                     thickness = 1.0,
                     radius = r,
                     radius_patch = R,
                     specific_storage_inner = s_1,
                     specific_storage_outer = s_2,
                     hydraulic_conductivity_inner = t_1,
                     hydraulic_conductivity_outer = t_2,
                     n_stehfest = 12L) |>
  plate()

dim_time_scale = (4.0 * t_1) / (s_1 * r^2)
dim_s_scale = 4.0 * pi * t_1 / q
bh$dim_time <- bh$time * dim_time_scale
bh$dim_s <- bh$aquifer_patch * dim_s_scale

plot(dim_s~dim_time, bh, type = "l", 
     ylab = "drawdown (dimensionless)", 
     xlab = "time (dimensionless)",
     log = "x",
     ylim = c(0, 50))

bh = recipe(formula = formula, data = dat) |>
  step_aquifer_patch(time = time, 
                     flow_rate = q,
                     thickness = 1.0,
                     radius = r,
                     radius_patch = R,
                     specific_storage_inner = s_1,
                     specific_storage_outer = s_2,
                     hydraulic_conductivity_inner = t_1,
                     hydraulic_conductivity_outer = t_2 * 10,
                     n_stehfest = 12L) |>
  plate()

dim_time_scale = (4.0 * t_1) / (s_1 * r^2)
dim_s_scale = 4.0 * pi * t_1 / q
bh$dim_time <- bh$time * dim_time_scale
bh$dim_s <- bh$aquifer_patch * dim_s_scale


points(dim_s~dim_time, bh, type = "l")
t_1 <- t_1 * 10.0
bh = recipe(formula = formula, data = dat) |>
  step_aquifer_patch(time = time, 
                     flow_rate = q,
                     thickness = 1.0,
                     radius = r,
                     radius_patch = R,
                     specific_storage_inner = s_1,
                     specific_storage_outer = s_2,
                     hydraulic_conductivity_inner = t_1,
                     hydraulic_conductivity_outer = t_2,
                     n_stehfest = 12L) |>
  plate()

dim_time_scale = (4.0 * t_1) / (s_1 * r^2)
dim_s_scale = (4.0 * pi * t_1) / q
bh$dim_time <- bh$time * dim_time_scale
bh$dim_s <- bh$aquifer_patch * dim_s_scale


points(dim_s~dim_time, bh, type = "l")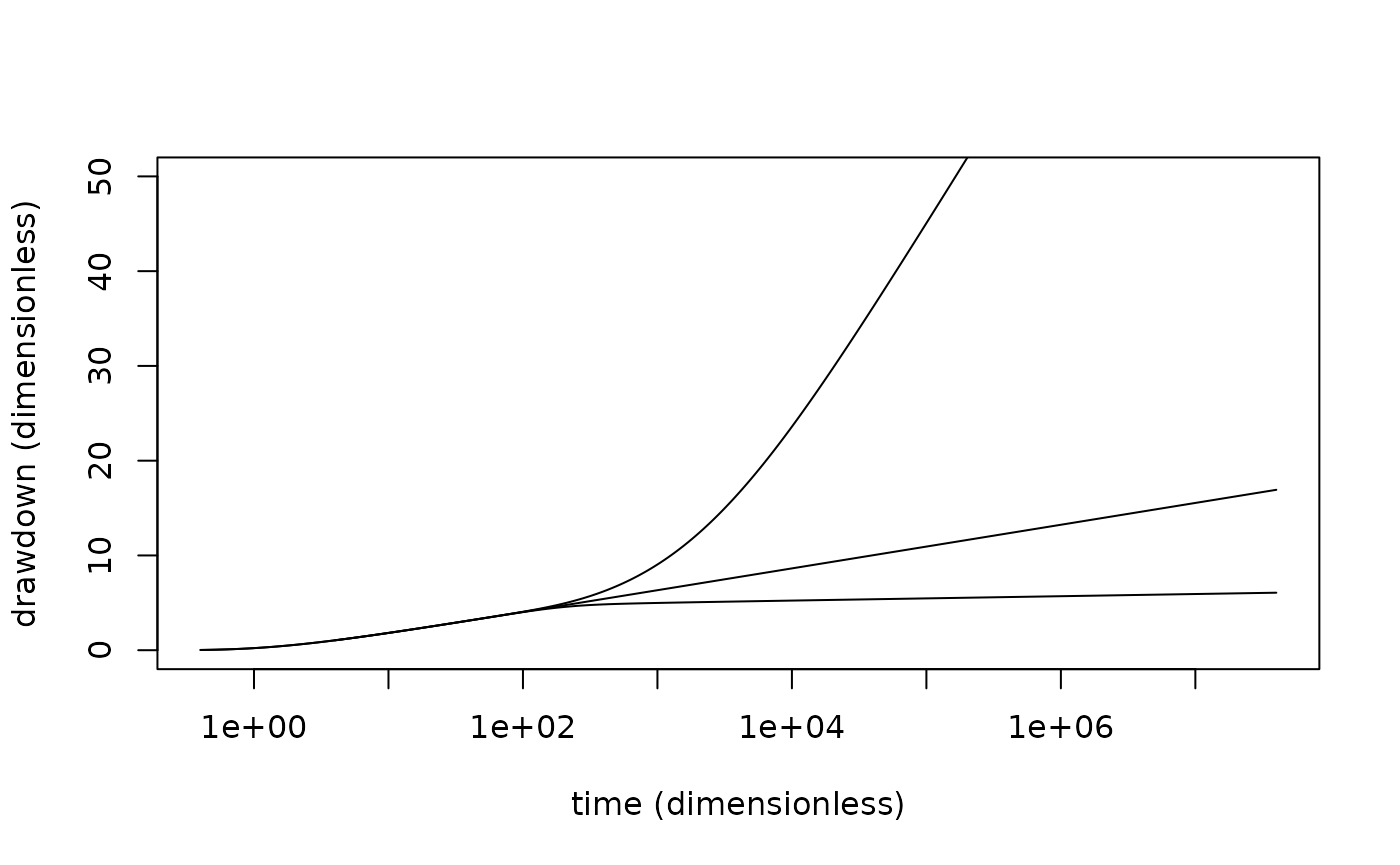

Dimensionless drawdown curves to match the Barker-Herbert, 1982 figure 3.

Figure 4 


formula <- as.formula(flow_rate~time)
q <- 0.05
t_1 <- 1.0
t_2 <- 1.0
s_1 <- 1e-5
s_2 <- 1e-5
r <- 100
R <- 90

bh = recipe(formula = formula, data = dat) |>
  step_aquifer_patch(time = time, 
                     flow_rate = q,
                     thickness = 1.0,
                     radius = r,
                     radius_patch = R,
                     specific_storage_inner = s_1,
                     specific_storage_outer = s_2,
                     hydraulic_conductivity_inner = t_1,
                     hydraulic_conductivity_outer = t_2,
                     n_stehfest = 14L) |>
  plate()

dim_time_scale = (4.0 * t_1) / (s_2 * r^2)
dim_s_scale = 4.0 * pi * t_2 / q
bh$dim_time <- bh$time * dim_time_scale
bh$dim_s <- bh$aquifer_patch * dim_s_scale

plot(dim_s~dim_time, bh, type = "l", 
     ylab = "drawdown (dimensionless)", 
     xlab = "time (dimensionless)",
     log = "x",
     ylim = c(0, 10))

bh = recipe(formula = formula, data = dat) |>
  step_aquifer_patch(time = time, 
                     flow_rate = q,
                     thickness = 1.0,
                     radius = r,
                     radius_patch = R,
                     specific_storage_inner = s_1,
                     specific_storage_outer = s_2,
                     hydraulic_conductivity_inner = t_1,
                     hydraulic_conductivity_outer = t_2 * 10,
                     n_stehfest = 14L) |>
  plate()

dim_time_scale = (4.0 * t_2 * 10) / (s_1 * r^2)
dim_s_scale = 4.0 * pi * t_2 * 10 / q
bh$dim_time <- bh$time * dim_time_scale
bh$dim_s <- bh$aquifer_patch * dim_s_scale


points(dim_s~dim_time, bh, type = "l")

bh = recipe(formula = formula, data = dat) |>
  step_aquifer_patch(time = time, 
                     flow_rate = q,
                     thickness = 1.0,
                     radius = r,
                     radius_patch = R,
                     specific_storage_inner = s_1,
                     specific_storage_outer = s_2,
                     hydraulic_conductivity_inner = t_1 * 10,
                     hydraulic_conductivity_outer = t_2,
                     n_stehfest = 14L) |>
  plate()

dim_time_scale = (4.0 * t_2) / (s_1 * r^2)
dim_s_scale = (4.0 * pi * t_2) / q
bh$dim_time <- bh$time * dim_time_scale
bh$dim_s <- bh$aquifer_patch * dim_s_scale


points(dim_s~dim_time, bh, type = "l")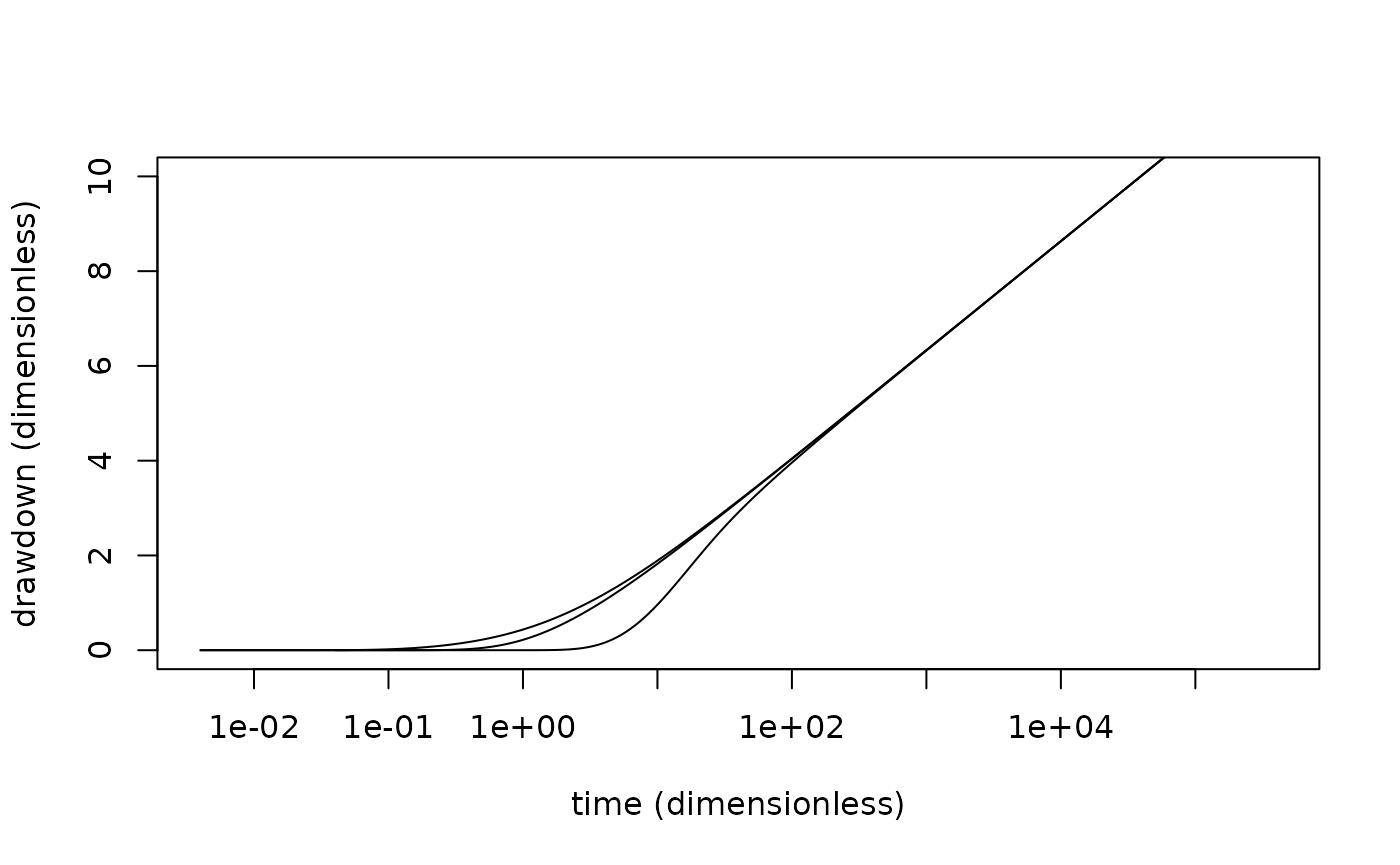

Dimensionless drawdown curves to match the Barker-Herbert, 1982 figure 4.

Papadopulos-Cooper wellbore storage(Papadopulos-Cooper, 1967) 



dat <- data.frame(time = 10^seq(-5, 2, length.out = 100),
                  flow_rate = rep(10.0, 100))
formula <- as.formula(flow_rate~time)

pc = recipe(formula = formula, data = dat) |>
  step_aquifer_wellbore_storage(time = time,
                                flow_rate = 10.0,
                                radius = 10.0,
                                radius_casing = 0.3,
                                radius_well = 0.3,
                                thickness = 1.0,
                                specific_storage = 1e-4,
                                hydraulic_conductivity = 1.0,
                                n_terms = 12L) |>
  plate()


th <- recipe(time~flow_rate, dat) |>
  step_aquifer_grf(time = time,
                   flow_rate = flow_rate,
                   thickness = 1.0,
                   radius = 10.0,
                   specific_storage = 1e-4,
                   hydraulic_conductivity = 1.0,
                   flow_dimension = 2.0) |>
  plate()

plot(aquifer_wellbore_storage~time, pc, 
     type = "l",
     log = "x",
     ylab = "drawdown", 
     xlab = "elapsed time")
points(aquifer_grf~time, th, type = "l", col = "darkgrey", lty = "dashed")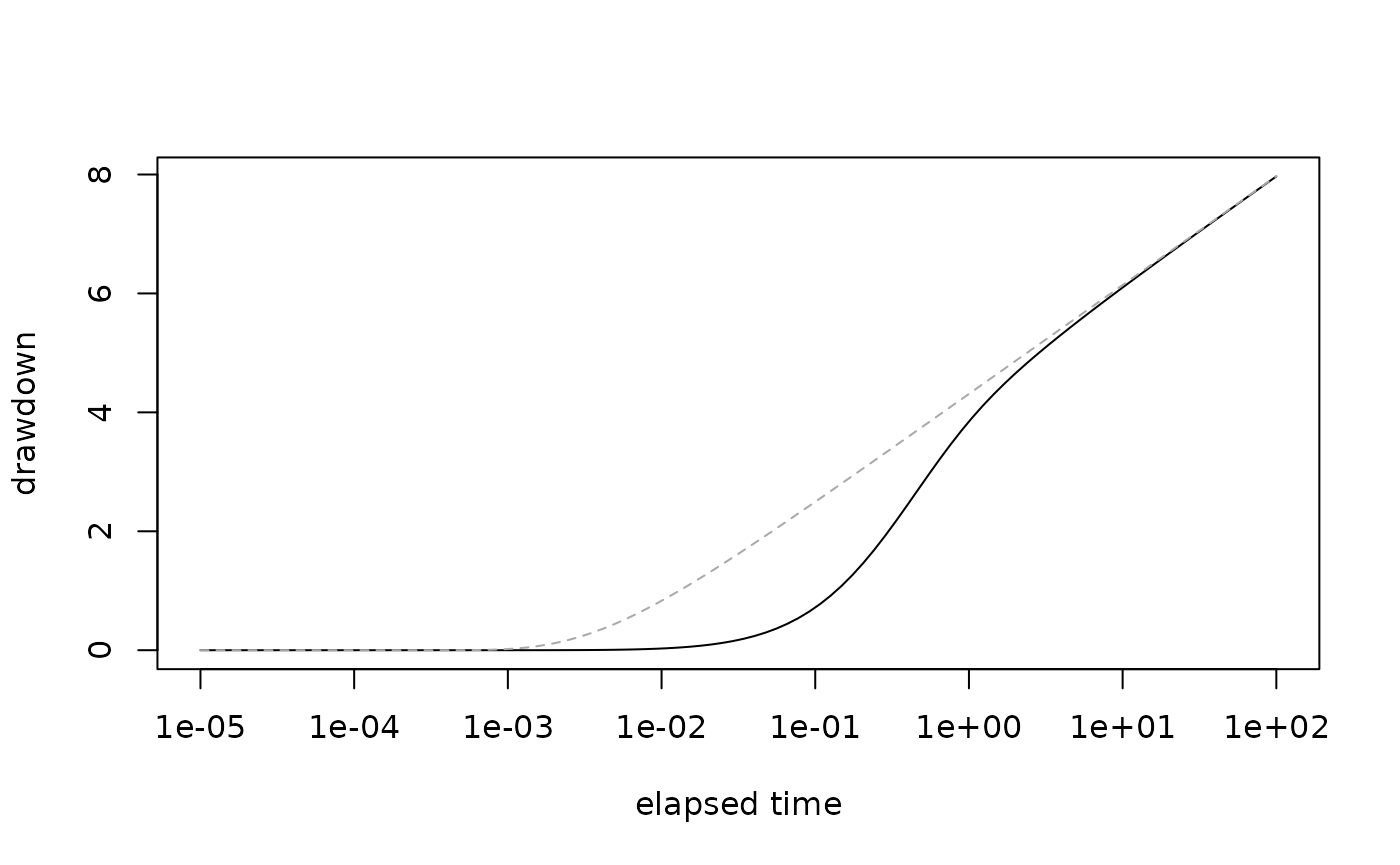

Drawdown curve showing delayed drawdown relative to the Theis solution due to wellbore storage.

Jacob-Lohman constant drawdown (Jacob-Lohman, 1952) 


time <- 10^seq(-5, 2, 0.1)
form <- formula(time~.)
dat <- data.frame(time = time)


jl = recipe(formula = form, data = dat) |>
  step_aquifer_constant_drawdown(time = time,
                                 drawdown = 10,
                                 thickness = 10,
                                 radius_well = 0.15,
                                 specific_storage = 1e-6,
                                 hydraulic_conductivity = 1) |>
  plate()

plot(aquifer_constant_drawdown~time, jl, type = "l", 
     ylab = "flow rate", 
     xlab = "elapsed time",
     log = "x")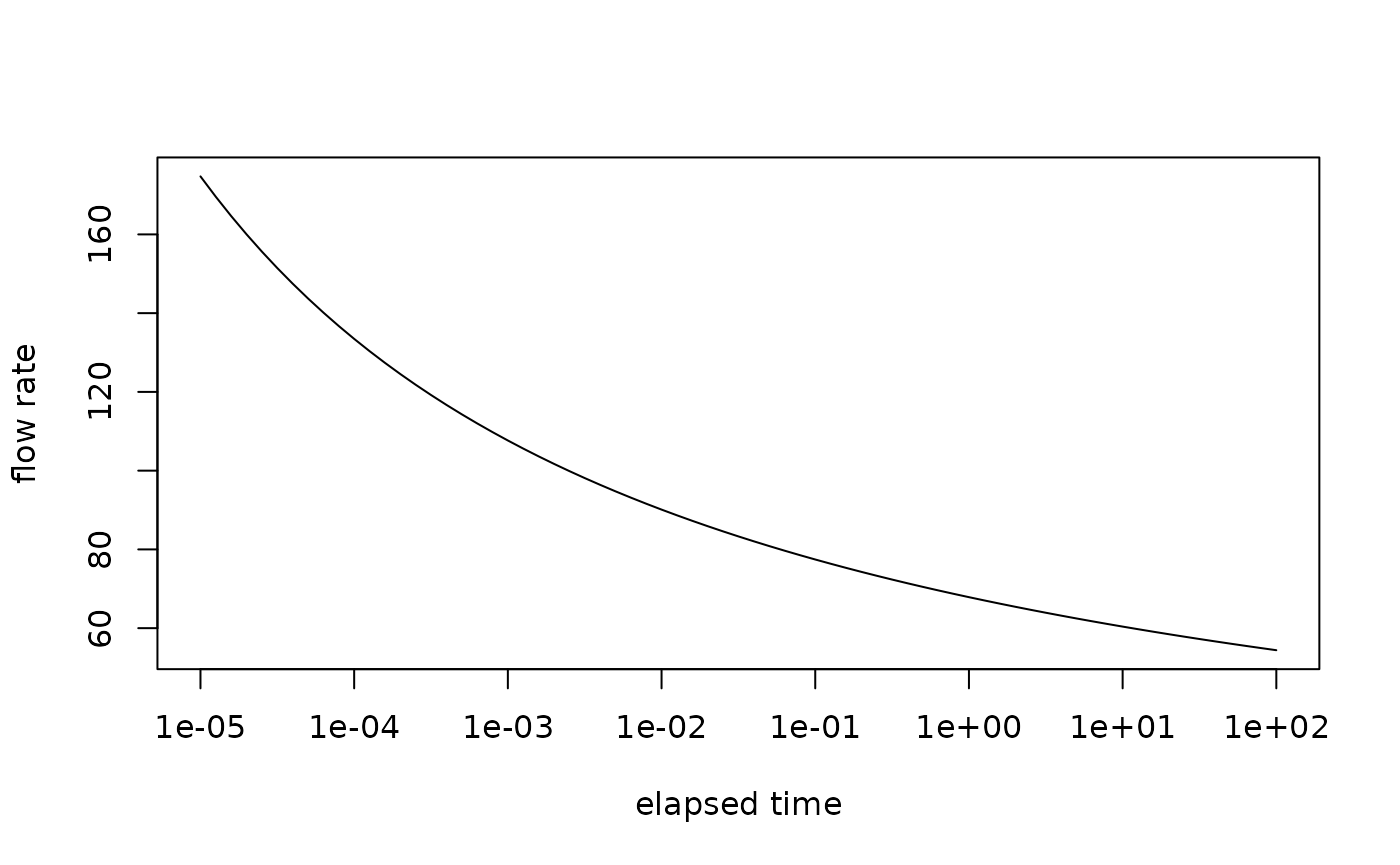

Flow rate declining with elapsed time and constant head pumping.

References

Barker, J.A., A generalized radial flow model for hydraulic tests in fractured rock. Water Resour. Res., 24 (1988), pp. 1796-1804, 10.1029/WR024i010p01796

Barker, J.A., and R. Herbert, 1982: Pumping tests in patchy aquifers, Ground Water, vol. 20, No. 2, pp. 150-155.

Butler, J.J., 1988: Pumping tests in nonuniform aquifers – The radially symmetric case, Journal of Hydrology, Vol. 101, pp. 15-30.

Hantush, M.S. and C.E. Jacob, 1955. Non-steady radial flow in an infinite leaky aquifer, Am. Geophys. Union Trans., vol. 36, no. 1, pp. 95-100.

Heilweil, V.M. and Hsieh, P.A., 2006. Determining anisotropic transmissivity using a simplified Papadopulos method. Groundwater, 44(5), pp.749-753.

Jacob, C.E. and S.W. Lohman, 1952. Nonsteady flow to a well of constant drawdown in an extensive aquifer, Trans. Am. Geophys. Union, vol. 33, pp. 559-569.

Papadopulos, I.S., 1965. Nonsteady flow to a well in an infinite anisotropic aquifer.

Papadopulos, I.S. and H.H. Cooper, 1967. Drawdown in a well of large diameter, Water Resources Research, vol. 3, no. 1, pp. 241-244.

Prodanoff, J.H.A., Mansur, W.J. and Mascarenhas, F.C.B., 2006. Numerical evaluation of Theis and Hantush-Jacob well functions. Journal of hydrology, 318(1-4), pp.173-183.

sessionInfo()
#> R version 4.4.2 (2024-10-31)
#> Platform: x86_64-pc-linux-gnu
#> Running under: Ubuntu 24.04.1 LTS
#> 
#> Matrix products: default
#> BLAS:   /usr/lib/x86_64-linux-gnu/openblas-pthread/libblas.so.3 
#> LAPACK: /usr/lib/x86_64-linux-gnu/openblas-pthread/libopenblasp-r0.3.26.so;  LAPACK version 3.12.0
#> 
#> locale:
#>  [1] LC_CTYPE=C.UTF-8       LC_NUMERIC=C           LC_TIME=C.UTF-8       
#>  [4] LC_COLLATE=C.UTF-8     LC_MONETARY=C.UTF-8    LC_MESSAGES=C.UTF-8   
#>  [7] LC_PAPER=C.UTF-8       LC_NAME=C              LC_ADDRESS=C          
#> [10] LC_TELEPHONE=C         LC_MEASUREMENT=C.UTF-8 LC_IDENTIFICATION=C   
#> 
#> time zone: UTC
#> tzcode source: system (glibc)
#> 
#> attached base packages:
#> [1] stats     graphics  grDevices utils     datasets  methods   base     
#> 
#> other attached packages:
#> [1] hydrorecipes_0.0.6 Bessel_0.6-1      
#> 
#> loaded via a namespace (and not attached):
#>  [1] cli_3.6.3         knitr_1.49        rlang_1.1.5       xfun_0.50        
#>  [5] textshaping_1.0.0 data.table_1.16.4 jsonlite_1.8.9    htmltools_0.5.8.1
#>  [9] earthtide_0.1.7   gslnls_1.4.1      ragg_1.3.3        sass_0.4.9       
#> [13] gmp_0.7-5         rmarkdown_2.29    grid_4.4.2        evaluate_1.0.3   
#> [17] jquerylib_0.1.4   fastmap_1.2.0     yaml_2.3.10       lifecycle_1.0.4  
#> [21] compiler_4.4.2    fs_1.6.5          htmlwidgets_1.6.4 Rcpp_1.0.14      
#> [25] lattice_0.22-6    systemfonts_1.2.1 digest_0.6.37     collapse_2.0.19  
#> [29] R6_2.5.1          parallel_4.4.2    Matrix_1.7-1      bslib_0.8.0      
#> [33] tools_4.4.2       Rmpfr_1.0-0       RcppThread_2.2.0  pkgdown_2.1.1    
#> [37] cachem_1.1.0      desc_1.4.3